山口行治(やまぐち・ゆきはる)
株式会社エルデータサイエンス代表取締役。元ファイザーグローバルR&Dシニアディレクター。ダイセル化学工業株式会社、呉羽化学工業株式会社の研究開発部門で勤務。ロンドン大学St.George’s Hospital Medical SchoolでPh.D取得(薬理学)。東京大学教養学部基礎科学科卒業。中学時代から西洋哲学と現代美術にはまり、テニス部の活動を楽しんだ。冒険的なエッジを好むけれども、居心地の良いニッチの発見もそれなりに得意とする。趣味は農作業。日本科学技術ジャーナリスト会議会員。
「データを回す」のは難しい。前回「住まいの多様体(その2)」の話題のように、ドアの出入りのデータを、2値化された波動とみなすと回転し始める。しかし積極的に「回して」いるとは言い難い。出入りは二つの状態を持っているけれども、一つの変数でしかない。二つ以上の変数の関係について「回転」を見いだすことで、1変数であっても回るコマの運動に一般化する方針で、多少遠回りをしてみよう。
◆相関係数には不満がたくさんある
統計学の勉強を始めると、1変数の平均や分散の話から、多変数の相関(共分散)の話に数式だけで進んでしまうことが多い。分散と共分散は形式的には同じような数式であらわされて、ともにデータのばらつきを表現している。統計が苦手だと思う人は、平均値の変化や比率の変化に注目しても、分散の変化を見逃すことが多い。筆者のように、職業としてデータ解析を行っていると、分散や共分散に注目してデータの全体を見渡してから、最終的に平均値や比率としてデータを集計する。データのばらつき具合は人為的にコントロールしにくいので、騙(だま)されることが少ないからだ。
臨床試験では数百の変数をデータ解析する。相関(共分散)は2変数の組み合わせの数だけあるので、例えば100変数であれば4950個の共分散が計算できる。これは極端な仮想的な話で、実際は科学的な観点から、もっと要因が絞られる。試験の主要な目的が薬効の評価だとすると、薬効に影響を与えるかもしれない要因X1-Xnを共変量としてデータ解析する。薬効は治療前後の症状の改善程度で評価する場合もあるけれども、二つの治療群に無作為に割り付けて、グループ間の症状改善度の差として評価することを統計専門家は好む。無作為に割り付けるという「ランダム化」がとても強力な統計学的方法となっている。素数のランダム性の奥義を究めるリーマン予想(※参考1)が証明されれば、「ランダム化」はとても強力な数学的方法と評されるようになるかもしれない。いずれにしても、薬効評価は多数の要因により複雑な影響を受けるので、共分散を注意深く評価する必要がある。
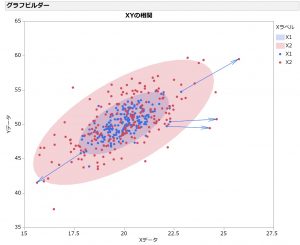
二つの変数の関係を分散図で評価してみよう。Xは平均値20、標準偏差1.0、Yは平均値50、標準偏差2.0の正規分布をすると仮定して、XとYが相関係数0.7で相関している場合を乱数でシミュレートしてみた。実際はXを正規乱数で作成し、YはXを与えた条件付き分布として作成している。このXYの分布はかなりバラツキが小さい。そこで、治療の後にXYそれぞれが2倍平均値から外れるように変化させて、重ね書きしてみた。
中央の青い楕円がXYの95%信頼領域(信頼水準95%の確率楕円)で、外の赤い楕円が平均値からの差が2倍となったデータの95%信頼領域になる。青い点から赤い点への矢印が個々のデータの変化を示している。このような変化では、相関係数は変化しない。
◆回る相関係数
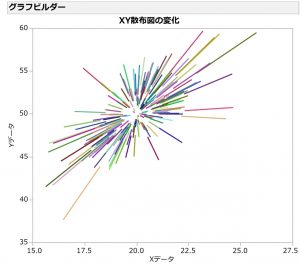
前図と同じデータで、全ての変化を線でつなぐと(前図の矢印に相当)、爆発する銀河のような図になる。このような変化が投薬の前後で見られたら、大きな問題だろう。例えば、急性薬剤性肝障害の可能性を調べるために、ASTとALTという肝機能関連の臨床検査値の分散図を描いて、投薬前後の変化を見たことがある。この図はその時の印象から作ってみた。
相関係数を見ていたのでは何もわからないし、共分散は大きくなるだけで、実際の変化をとらえることはできない。この図をベクトル場としてみると、爆発している場合もあれば、回転している場合もあるかもしれない。ベクトル場というと数学的には難しくなるが、ベクトル場は流れを可視化していると比喩(ひゆ)的に理解することができる。多変量統計学の方法では、多数の変量を縮約して、少数次元で理解しやすいように変換する場合が多い。実用的には主成分分析(※参考2)が代表的な例になる。本論では独立成分分析(※参考3)を拡張して応用することを企てている。共分散行列の性質から数学的な操作で縮約するのだけれども、爆発や回転などの物理的なイメージは消滅してしまう。データ解析に力学的な方法を応用することで、特に健康データなどの時間に依存するデータから、見落とされていた特徴を捉えることができるだろう。分散図をベクトル場として再考することから始まり、特に微分方程式としての解がよく研究されている「コマの運動」との関連を考えてみたい。
「自転するコマの運動」の代表例は、太陽の周りをまわる地球の楕円運動で、最も古典的な運動方程式の例であるとともに、微分方程式の解の構造を代数的に研究することで、位相幾何学などの現代数学を推進してきた重要な課題だ。数学に確率やカオスが導入されて以来、微分方程式を解くのは古典的な課題となってしまったが、コマの回転運動を数学的な意味で一般化して、空間や時間を離散化すると、計算機科学にとって重要な課題として再浮上してきた。データ解析も計算機科学の傍流になるので、「データを回す」ための数学的な手掛かりをコマの幾何学に求めてみた。『コマの幾何学―可積分系講義』(Michele Audin著、共立出版、2000年)は筆者の書棚に数年間埋もれていた。量子論的な回転場であるスピノールの理論を理解するために、古典物理のスピンについて勉強するつもりだったが、数学的にはとても深く、数学を専門的に楽しむ素晴らしい教科書であった。なによりも、スピノールでは望むべくもない、計算機科学との接点があったのは幸運だった。しかし、筆者の数学力でこの教科書を理解できるようになるのは、かなりの未来のことだろう。気長に取り組んでゆきたい。
◆回る連想記憶
日常生活は様々な雑務に流され、日々クルクル回っているだけという印象を持って生きているのは筆者だけではないだろう。ところが、リハビリテーション医療や障害者福祉の原点ともいうべき、ICF(国際生活機能分類)の「国際生活機能分類-国際障害分類改訂版-」(※参考4)においては「回る」機能や構造は全く現れてこない。体系的な分類方法なのだから仕方がないと言ってしまえばそれまでだが、生き続けるための生活実感とはほど遠いものになっている。
ICFのように普及していないが、日本でもユニークな研究がある。東北福祉大学の「元気点検表」(※参考5)では元気姿勢スコアとして、元気点検表の前回値と今回値の変化量に注目している。筆者も山本光璋(やまもと・みつあき)教授のお誘いで、データ解析関連とNPO法人化などの検討に参画したことがある。すでに10年以上前からのお付き合いになるが、その時には「データを回す」アイデアは生まれていなかった。しかし「元気共鳴装置」として、より元気になる努力を支援する仕組みを考えたことがある。See-Think-Plan-Doのようなサイクルを回しながら、仲間とデータを共有して励ましあう仕組みだ。仲間としてはモノのインターネットIoTの可能性として、炊飯器などの家電製品による支援を想定して「元気共鳴装置」と名付けていた。共鳴するためには波動なり回転することが不可欠なので、もう少しで「データを回す」ことに思い至っていただろう。
例えば記憶障害について考えてみよう。記憶力といっても、トランプゲームの「神経衰弱」のように、意味のないものを記憶することは日常生活ではほとんどない。多くの場合、ある場面の一部として、または時間継起の連鎖として記憶している。ある場面の一部に意識が集中したときに、その部分が拡大したり揺れ動いたりして、深い印象と共に記憶される。様々な事象の連鎖においても、それは線形的な連鎖ではなく、異質なものが継起する「はっと振り向いた」ときのような、遠心力を伴う連鎖により、物理的に記憶してしまう。連鎖としての記憶を「連想記憶」と呼ぶとすると、連想記憶は回っている。記憶障害において、連想記憶が回らなくなること、日常生活が回らなくなることが要因になっている可能性は多分にあるだろう。日常生活が回るようになれば、少なくとも日常生活に必要な程度の記憶力が回復するかもしれない。日常生活が回る空間は「住まいの多様体」であり、自己の延長された表現型(またはニッチ構築)なのだから、他者から与えられるものではなく、他者と共に作り出してゆく空間であって、もともと動的な性格を伴っている。
◆目標を設定すること、達成すること
人生の目標を自ら設定することは困難で、達成することはほぼ不可能なように思われる。しかし何らかの病的な状態、もしくは健康リスクが高い状態においては、目標は医学的に設定されていて、その達成方法が現代医学では不十分という状況がよくある。筆者は医薬品の臨床試験データを解析する仕事に従事しているので、プラセボ(偽薬)の使用が倫理的に問題ないことを信じて仕事をしている。筆者の理解では、最も信頼できる診断が行われ、薬物療法以外の適切な医療が提供されることが倫理的判断の条件となる。例えば認知症の薬物療法の場合、必ずしも最も信頼できる脳機能画像診断が行われるわけではないし、薬物療法以外の適切な医療とは何かよくわからない。それでもプラセボを使うことが倫理的と判断されるためには、新薬への高い期待値と副作用への注意深い対応が不可欠で、なかなか新薬の開発が成功しない。プラセボを使わない新しい臨床試験の方法論を思考実験しながら、本稿を書き進めている。
慢性疾患における予防医療の取り組みを、リハビリテーション医療の枠組みで再考することで、上述のようなプラセボを使わない臨床試験デザインのヒントが得られるのではないかと考えている。図書館でリハビリテーション医療を勉強すると、その大半がICFの解説から始まる。しかし、びっくりするほど先験的な著書もあった。『私の精神障害リハビリテーション論』(蜂谷英彦、金剛出版、2016年)には、「精神科領域では、病気と障害が同時に並行して進む。だから障害が固定してからリハビリをやるのでは遅い」と明記されている。統合失調症が分裂病と呼ばれ、不治の病であった時代の臨床哲学である。認知症も不治の病ではなくなる時代になるはずだ。薬物療法と調和した認知症のリハビリテーション論はどのようなものになるのだろうか。
ICFでは1424項目の健康関連の生活機能分類項目が定義されている。これらの項目は中分類、大分類に分類されるので、完全に独立な項目ではないが、例えば認知症患者の生活環境マップを作成し、リハビリテーションの立場から問題点を明確にして治療目標を設定するのにはよい出発点になるはずだ。当面の治療目標は単項目として、目標を達成するための薬剤処置の効果を環境因子(共変量)によって調整(予測)する場合、生活機能関連の共変量は100変量程度だろうか。いずれにしても、この超多変量を2次元か3次元に縮約して、目標を達成するルートを見いだすことになるだろう。
◆複素数の実在性
人は何かを信じる。プラセボの倫理的判断を信じる、神の存在と宗教の有用性を信じる、1+1=2を信じる、お金が力であると信じる。それぞれ信じる程度や内容は異なっても、信じるという行為には共通の何かがあるのだろう。筆者は複素数の実在性を信じている。そうは言っても実数の実在性をあまり信じていないので、正確には虚数単位で拡大した有理数体(ガウス数体)の実在性を信じているのかもしれない。もっと別の拡大体はよくわかっていないだけのことなのだろう。複素数の実在性を信じるということは、波動とか拡散という現象を示す物質の実在性の根本に複素数があって、複素数なしにはこれらの現象を理解できないと信じていることだ。
exp(iθ)=cosθ+i‣sinθ(複素数の極形式を示すオイラーの公式)が本質的で、1+1=2は近似的な論理による人工世界なのだ。だから世界は回っていると信じている。古典論理の世界は回らない。もっとも、素数の世界が回っていることが明らかになれば(リーマン予想)、古典論理の世界も回りだすかもしれない。
量子計算機が実現されない限り、現在の計算機は古典論理の世界だ。計算機が古典論理で設計されていても、計算機に記憶されたデータは実在世界の性質を反映しているから、人の感覚を超える膨大な量のデータ(アボガドロ数のオーダー)を超高速に計算すると(1秒に1兆回以上の浮動小数点演算)その世界は古典論理の枠に収まるとは限らない。だから筆者は「データは回る」と信じている。迷信かもしれないけれども、新興宗教にはしたくない。実際に役立つ応用があるはずだと信じている。
参考1;リーマン予想
https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%BC%E3%83%9E%E3%83%B3%E4%BA%88%E6%83%B3
参考2;主成分分析
https://ja.wikipedia.org/wiki/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
参考3;独立成分分析
https://ja.wikipedia.org/wiki/%E7%8B%AC%E7%AB%8B%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
参考4;国際生活機能分類-国際障害分類改訂版-(日本語版)の厚生労働省ホームページ掲載について
http://www.mhlw.go.jp/houdou/2002/08/h0805-1.html
参考5;東北福祉大学tfu元気点検表
https://www.tfu.ac.jp/special/genki/score.html











コメントを残す